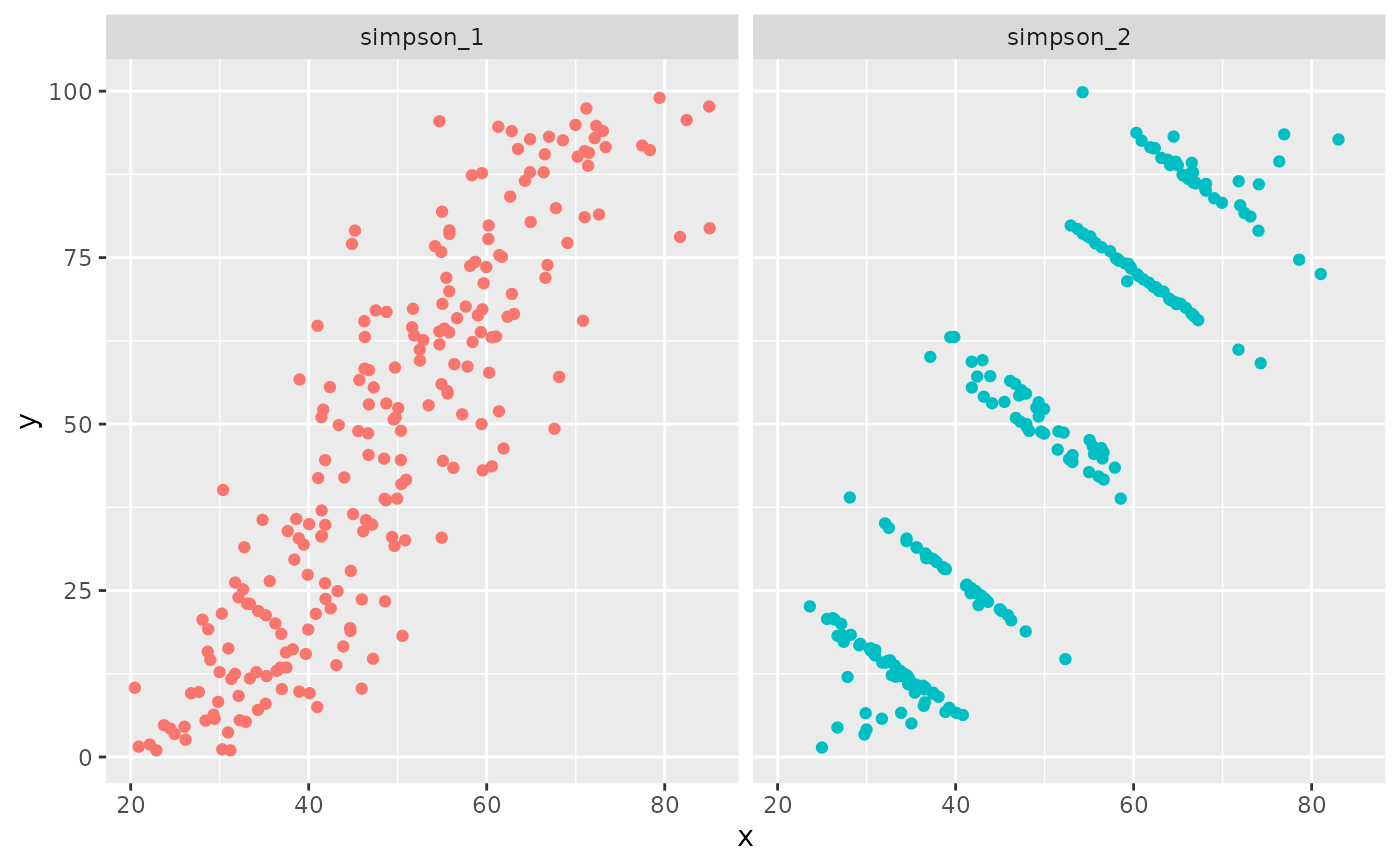
A dataset demonstrating Simpson's Paradox with a strongly positively correlated dataset (simpson_1)
and a dataset with the same positive correlation as simpson_1, but where individual groups have a
strong negative correlation (simpson_2).
Format
A data frame with 444 rows and 3 variables:
dataset: indicates which of the two datasets the data are from,
simpson_1orsimpson_2x: x-values
y: y-values
References
Matejka, J., & Fitzmaurice, G. (2017). Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing. CHI 2017 Conference proceedings: ACM SIGCHI Conference on Human Factors in Computing Systems. Retrieved from https://www.autodeskresearch.com/publications/samestats.
Examples
if(require(ggplot2)){
ggplot(simpsons_paradox, aes(x=x, y=y, colour=dataset))+
geom_point()+
theme(legend.position = "none")+
facet_wrap(~dataset, ncol=3)
}
 # Base R Plots
state <- par('mfrow')
par(mfrow = c(1, 2))
sets <- unique(datasaurus_dozen$dataset)
for (i in 1:2) {
df <- simpsons_paradox[simpsons_paradox$dataset == paste0('simpson_', i), ]
plot(df$x, df$y, pch = 16, xlab = '', ylab = '')
title(paste0('Simpson\'s Paradox ', i))
}
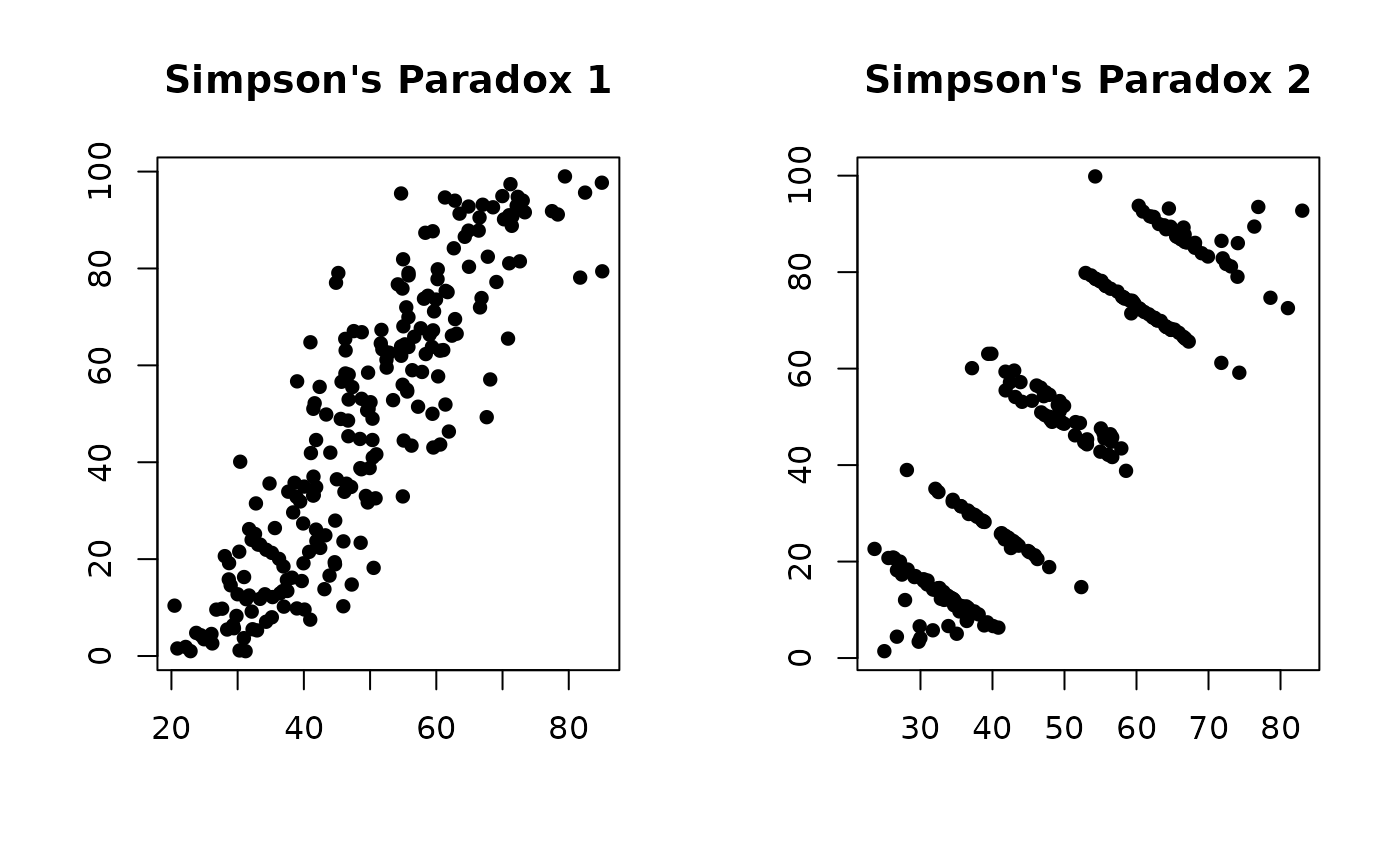
# Base R Plots
state <- par('mfrow')
par(mfrow = c(1, 2))
sets <- unique(datasaurus_dozen$dataset)
for (i in 1:2) {
df <- simpsons_paradox[simpsons_paradox$dataset == paste0('simpson_', i), ]
plot(df$x, df$y, pch = 16, xlab = '', ylab = '')
title(paste0('Simpson\'s Paradox ', i))
}
 par(state)
#> NULL
par(state)
#> NULL
